On 16 September 2018, the worst nightmare for programmers at food delivery app Deliveroo came true…
Customers were charged multiple times for the same food items. Food wasn’t delivered on time or not at all. And Deliveroo? Deliveroo was being bombarded with messages.
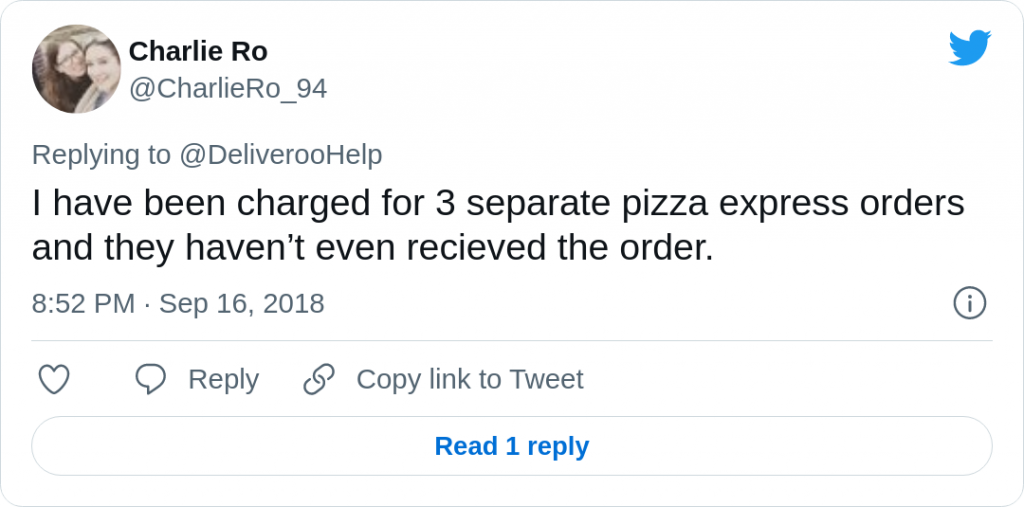
Let’s say that you want to order a pizza, just as @CharlieRo_94 did.
You place the order, and your phone sends a message to Deliveroo’s server.
In response to the message, Deliveroo sends you a payment request.
After you paid, your phone sent a confirmation back to the server. Everything is going according to plan.
But here’s the catch: the server never got that confirmation message.
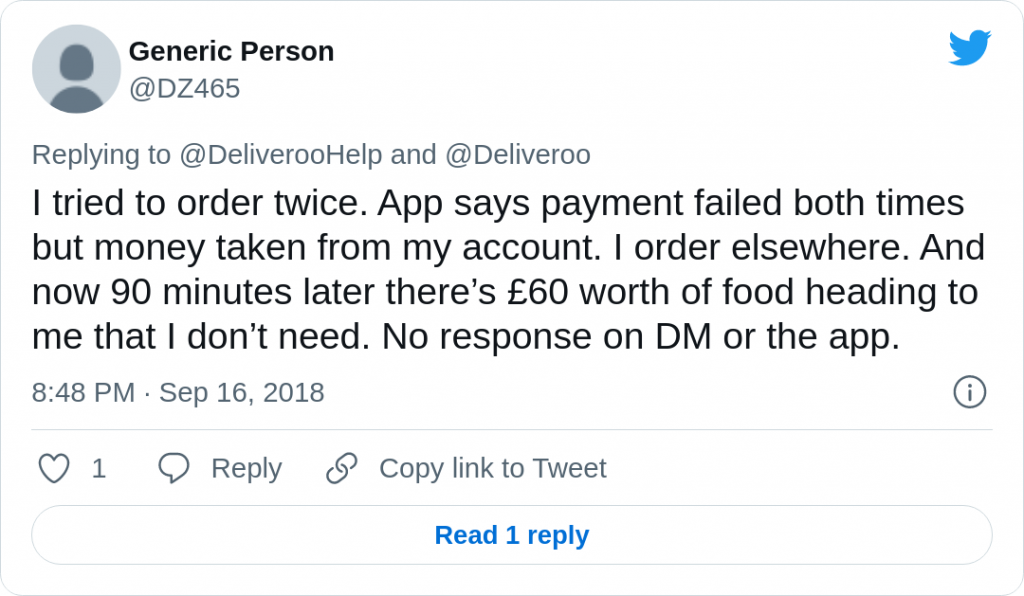
So what happens if the server responsible for checking if you paid does not receive the ‘this is paid’ message?
Well… after some time it sends a response to your phone: “PAYMENT FAILED”. Oh no, let’s try again.
But remember: you have already paid! The money was previously deducted from your bank account. By paying another time, the same amount of money will be retaken from your balance. 💸💸💸
And there are no guarantees that the server will receive the confirmation message this time. So clearly, something goes terribly wrong at Deliveroo’s servers. It is time for a classic Computer Science story that is told to every aspiring computer scientist.
Introducing...
The Two General's Problem
Picture yourself two army leaders. A green and a brown general, or a red and a blue one, whatever floats your boat. For the sake of simplicity, I’ll call them General A1 and General A2.
General A1
General A2
Generals A1 and A2 have a common enemy: a castle, located in the bottom of a valley.
And for me, this is the point where the analogy breaks down. WHO IN THEIR RIGHT MIND WOULD BUILD A CASTLE IN A VALLEY? That is just dumb. Everyone knows that building a castle on top of a hill is much more helpful since it can be defended easier.
Ahum, fine, let’s stay professional.
At some point, the two generals surround the castle. A1 and his army are located at the left side of the valley, whereas A2 with this army takes place on the right side of the valley.
Both generals know that they can only beat the hostile castle, if they attack at the exact same time. Sounds simple, but as it turns out: this is harder than you think. How would your coördinate such a raid? Or maybe a more specific question: how would you reach a consensus about the time to attack?
Messengers
Let’s assume A1 wants to initiate an invasion. He wants to make sure that A2 attacks at the same time, thus he sends a message to the other side of the valley. A conversation between A1 and A2 could look something like this:
For this analogy to work. we assume the message should be delivered by a messenger that travels from A1 to A2. All fun and games, until you realize what kind of path a potential messenger should take…
Right! Every messenger has to travel through the valley with the hostile castle. And it is not hard to imagine what the guards of the castle do when they intercept this messenger. 💀💀💀
Also: no cheating. Morse code, helicopters, or other creative approaches cannot be used.
Let’s continue. A1 sends a messenger through the valley:
A1’s messenger reaches A2’s camp safely. Disaster avoided.
Right?
Well, not really. Both A1 and A2 know that there is a chance that a message ‘gets lost’ on the way to the other side. Hence, A2 sends a confirmation message back to A1.
Oh noo! Our worst nightmare comes true. A2’s message is intercepted by the enemy.
Let’s look at the current status.
A2: has received A1’s plans for attack. He will thus attack at 10 PM.
A1: has not heard anything from A2. He assumes his original message was intercepted, and will thus abord his attack.
And that’s a problem! Because at this stage, only one army will attack, which results in a loss.
Now, what would happen if A2’s message makes it successfully to the other side of the valley?
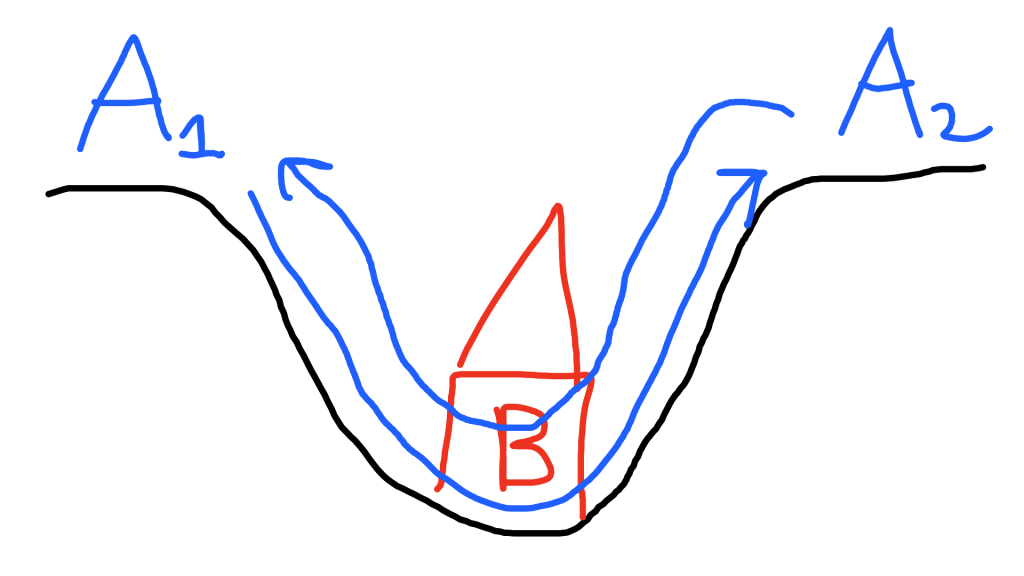
In that case, A1 knows that A2 has received the attack information correctly. However, due to the fact that messages could get lost, A2 now does not know if A1 has received his confirmation message!
How could this be solved? Well… A1 could send a message confirming A2’s message, starting the complete cycle all over again.
A paradox
This results in a paradox: no matter how many messages the generals would send back and forth, they would never know if a consensus on the time of attack is reached.
Back to Deliveroo
And this Two General’s Problem was exactly what happened that night on the 16th of September: Deliveroo’s acknowledgements did not arrive to the payment processors and Deliveroo app. Now we know why this causes chaos. Albeit no brave messengers died, @CharlieRo_94 did not receive her pizza. Which is equally as bad, right?
Aren’t there any solutions, then? Well, yes. There are. Deliveroo should never have accepted payments for an identical order from the same person placed within – let’s say – 30 minutes from the original order.
And there are more tricks. For example, Deliveroo can assign a unique order number to each order. If an order is already paid, but the customer tries to pay again, Deliveroo can resend the payment confirmation, instead of allowing a second payment. This resending of a confirmation is common practise in quite some modern (and older) internet protocols, such as the widely used Transmission Control Protocol (TCP)*. Reliable messaging is a study field on its own, and falls beyond the scope of this long-form story.
*Footnote: Although TCP does a great job at reliable data transfers, the protocol does not manage to solve the Two General’s Problem. The Two General’s Problem is a paradox that cannot be solved. Read more about it on StackOverflow.
Conclusion
To summarise, things went horribly wrong at Deliveroo’s servers on 16 September 2018. We have learned that the problems were caused by the Two General’s Problem: a paradox in computer science that states that two parties can never reach a consensus over an unreliable communication line. There are practical implementations that can be used to minimize the effect of this paradox, such as implementing a reliable messaging system.
THE END
Further reading
A reader from the University of Cambridge about Distributed Systems, aka the ‘real’ science behind this topic.
A short lecture on the Two General’s Problem by Martin Kleppmann, the author of the reader above.
Another short lecture, again by Martin Kleppmann, about an interesting variation on this paradox: The Byzantine General’s Problem.
Tom Scott’s video about the Two General’s Problem – he has more budget for graphics than I have.
The Wikipedia page about the Two General’s Problem, containing proofs, history, and ‘solutions’.
Credits, acknowledgements, and licence
Most of the information in this article is based on the earlier mentioned reader and lectures by Martin Kleppmann. This long-form type of story was inspired by Neal.fun. The tweets are courtesy of Twitter.com. All other graphics are drawn by the author. This website is built using WordPress, Elementor, and the Astra theme. The script for the ’emojisplosion’ is courtesy of Josh Goldberg.
The story and accompanying visuals can be freely shared under the BY-CC licence.
About the author
Stach Redeker is a student Electrical Engineering at the University of Twente in the Netherlands. He has a general interest in cybersecurity and works as a freelance WordPress developer. Lastly, Stach loves pizza – as long as it’s delivered on time, of course.
